Identify diamond structure¶

This analysis modifier finds atoms that are arranged in a cubic or hexagonal diamond lattice. This structure identification method has been described in Appendix A of

E. Maras et al.

Global transition path search for dislocation formation in Ge on Si(001)

Computer Physics Communications (2016)

doi:10.1016/j.cpc.2016.04.001

Please cite this paper when you use this structure identification algorithm for diamond lattices in your work. A preprint is available here.

The algorithm analyzes the local environment of each atom up to the second neighbor shell to determine the local structural type. The results are stored in the Structure Type particle property, with the type assigned to each atom encoded as an integer value:

Type Id	Type Name	Description
0	Other	Atom with unknown coordination structure, which doesn’t belong to any of the classes below.
1	Cubic diamond	Atom having all of its first and second nearest neighbors positioned on cubic diamond lattice sites.
2	Cubic diamond (1st neighbor)	Atom being a first neighbor of an atom that was classified as cubic diamond. Its four neighbors are positioned on lattice sites, but at least one of its second nearest neighbors is not.
3	Cubic diamond (2nd neighbor)	Atom being a second nearest neighbor of an atom that was classified as cubic diamond. The atom itself is positioned on a lattice site, but at least one of its neighbors is missing or is not positioned on a lattice site.
4	Hexagonal diamond	Atom having all of its first and second nearest neighbors positioned on hexagonal diamond lattice sites
5	Hexagonal diamond (1st neighbor)	Atom being a first neighbor of an atom that was classified as hexagonal diamond. Its four neighbors are positioned on lattice sites, but at least one of its second nearest neighbors is not.
6	Hexagonal diamond (2nd neighbor)	Atom being a second nearest neighbor of an atom that was classified as hexagonal diamond. The atom itself is positioned on a lattice site, but at least one of its neighbors is missing or is not positioned on a lattice site.

The option Use only selected particles restricts the analysis to the currently selected atoms. If this option is activated, unselected atoms will be ignored (as if they did not exist) and will be assigned the structure type “Other”. This option can be useful if you want to identify defects in a crystal with a non-diamond structure, but which has a sublattice that is a diamond lattice (and you do not want to delete atoms belonging to the other sublattice(s) for some reason).

How it works¶

To classify a central atom, this structure identification method takes into account second nearest neighbors to discriminate between cubic and hexagonal diamond structures. The method can be considered an extended version of the popular Common Neighbor Analysis (CNA), which is typically used to identify FCC, HCP, or BCC structures. However, the conventional CNA is not suited for diamond structures, because nearest neighbor atoms don’t have common neighbors, and the second and third nearest neighbor shells are not well separated.

Central atom (green), nearest neighbors (blue), and neighbors of neighbors (yellow):

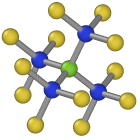
../../../_images/identify_diamond_cubic.png

Cubic diamond¶

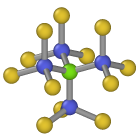
../../../_images/identify_diamond_hexagonal.png

Hexagonal diamond¶

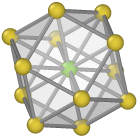
../../../_images/identify_diamond_cubic_fcc.png

FCC¶

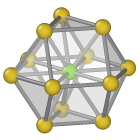
../../../_images/identify_diamond_hexagonal_hcp.png

HCP¶

These problems are solved as follows: First, the nearest neighbors of an atom are identified. Then, for each of these four neighbors, their respective nearest neighbors are identified. This yields the list of second nearest neighbors of the central atom. Finally, the CNA fingerprint is computed for these 12 second nearest neighbors and the central atom. If they are arranged on a FCC lattice, then the central atom is classified as cubic diamond. If they form a HCP structure, then the central atom is marked as an hexagonal diamond atom.

Further details can be found in the publication.